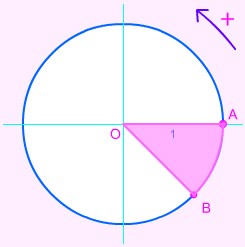
En vous aidant du cercle trigonométrique ci-dessous, complétez les phrases suivantes :
Lorsqu'on déplace le point B le long du cercle trigonométrique, les deux demi-droites [OA) et [OB) forment un
.
angle
Le cercle trigonométrique ayant un sens de parcours positif (sens direct), cet angle est un angle
.
orienté
orienté | non orienté
Si pour aller de A à B en prenant le plus court chemin sur le cercle, on tourne dans le sens direct, cet angle est
Il est
dans le cas contraire.
positif
positif | négatif
négatif
positif | négatif
On peut repérer cet angle par les abscisses curvilignes du point B (chemins orientés sur le cercle pour aller de A à B).
On appelle alors la mesure de cet angle mesure en
.
On appelle alors la mesure de cet angle mesure en
radian
unité de mesure
Si l'abscisse curviligne du point B est son abscisse curviligne principale alors la mesure de l'angle correspondant est sa mesure
, elle appartient à
.
principale
]-π;π]
intervalle
Exemples :
Qu'elle est la mesure en radians des angles roses suivants ainsi que leur mesure principale ?

Qu'elle est la mesure en radians des angles roses suivants ainsi que leur mesure principale ?

La mesure en radian de l'angle rose est égale au chemin orienté parcouru pour aller du point A au point B.
On peut aller du point A au point B en faisant 1/4 de tour dans le sens trigonométrique, le chemin parcouru est alors π/2.
Si on fait le même chemin en ajoutant un tour complet, le chemin est π/2+2π.
Si on retranche un tour complet, le chemin est π/2-2π.
En ajoutant deux tours complets le chemin est π/2+4π.
En retranchant deux tours complets le chemin est π/2-4π.
...
La mesure en radians de l'angle rose est donc : π/2+2kπ avec k∈z.
La mesure principale est celle comprise entre ]-π;π], c'est-à-dire : π/2.
On peut aller du point A au point B en faisant 1/4 de tour dans le sens trigonométrique, le chemin parcouru est alors π/2.
Si on fait le même chemin en ajoutant un tour complet, le chemin est π/2+2π.
Si on retranche un tour complet, le chemin est π/2-2π.
En ajoutant deux tours complets le chemin est π/2+4π.
En retranchant deux tours complets le chemin est π/2-4π.
...
La mesure en radians de l'angle rose est donc : π/2+2kπ avec k∈z.
La mesure principale est celle comprise entre ]-π;π], c'est-à-dire : π/2.

Pour aller du point A au point B, on peut faire 1/8 de tour dans le sens contraire au sens trigonométrique, le chemin orienté parcouru est alors -π/4.
En ajoutant un tour complet, le chemin est -π/4+2π.
...
La mesure en radians de l'angle rose est donc : -π/4+2kπ avec k∈z.
La mesure principale est celle comprise entre ]-π;π], c'est-à-dire : -π/4.
En ajoutant un tour complet, le chemin est -π/4+2π.
...
La mesure en radians de l'angle rose est donc : -π/4+2kπ avec k∈z.
La mesure principale est celle comprise entre ]-π;π], c'est-à-dire : -π/4.
